Mathematics reveals elegant patterns in unexpected places. Consider 1/998001, which equals 0.000001002003004… containing every three-digit number in sequence.
This occurs because 998001 = 999². Similar patterns emerge in related fractions:
- 1/9 = 0.111111…
- 1/99 = 0.010101…
- 1/999 = 0.001001001…
These numerical sequences demonstrate that mathematics is not merely computational but reveals fundamental structures underlying our universe. Such patterns have practical applications in algorithm development, cryptography, and data analysis.
The ordered nature of these mathematical curiosities reminds us that even within apparent complexity, we can discover remarkable simplicity and structure.
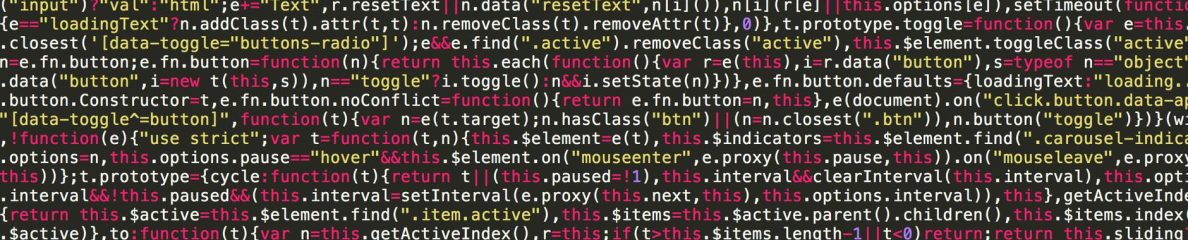
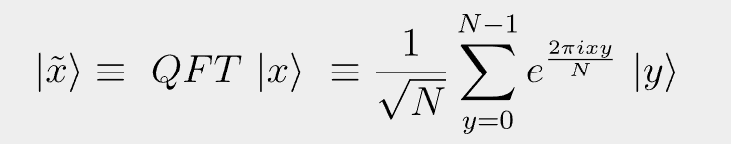
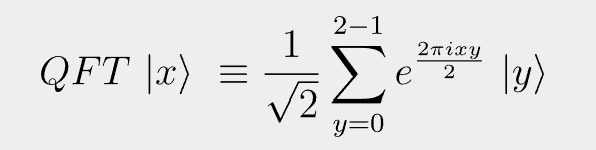
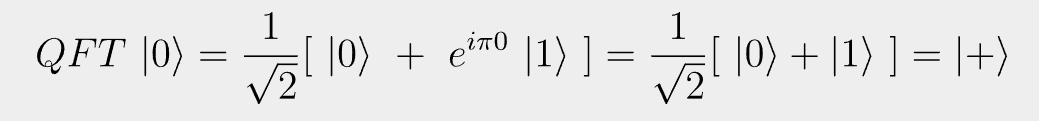
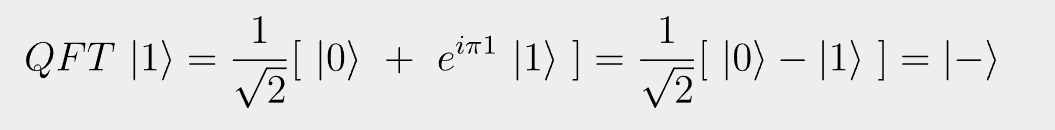
You must be logged in to post a comment.