Below is the definition of QFT as illustrated in the YouTube lecture by Abraham Asfaw.
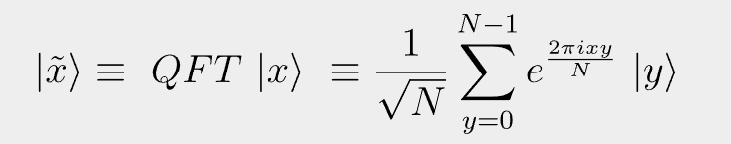
The LaTex code for the equation is as follows and also available here.
Latex
| \tilde{x} \rangle \equiv ~ QFT ~ |x \rangle ~ \equiv \frac{1}{\sqrt{N}}\sum_{y=0}^{N-1}{e^{\frac{2\pi ix y}{N}}} ~| y \rangleFor the one qubit case, N = 21 = 2:
Latex
| \tilde{x} \rangle \equiv ~ QFT ~ |x \rangle ~ \equiv \frac{1}{\sqrt{}N}\sum_{y=0}^{N-1}{e^{\frac{2\pi ix y}{N}}} ~| y \rangle
Latex
\frac{1}{\sqrt{2}}\sum_{y=0}^{1}{e^{\pi ix y}} ~| y \rangle = \frac{1}{\sqrt{2}}[~e^{i \pi x 0}~ | 0 \rangle ~ + ~ e^{i \pi x 1}~| 1 \rangle] = \frac{1}{\sqrt{2}}[~|0\rangle ~+~e^{i \pi x}~|1 \rangle~]Latex
QFT~| 0 \rangle = \frac{1}{\sqrt{2}}[~|0\rangle ~+~e^{i \pi 0}~|1 \rangle~] = \frac{1}{\sqrt{2}}[~| 0 \rangle + |1 \rangle~] = |+\rangleLatex
QFT~| 1 \rangle = \frac{1}{\sqrt{2}}[~|0\rangle ~+~e^{i \pi 1}~|1 \rangle~] = \frac{1}{\sqrt{2}}[~| 0 \rangle - |1 \rangle~] = |-\rangleHence the QFT of a single qubit is essentially the Hadamard transform.


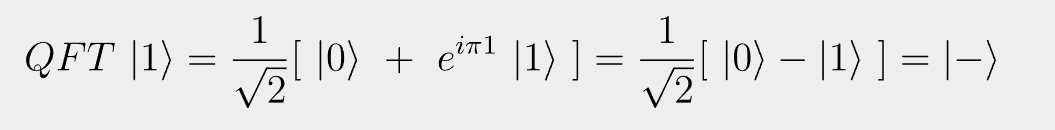
You must be logged in to post a comment.