Tag: quantum computing
Chinese Scientists Report Using Quantum Computer To Hack Military-grade Encryption
As Quantum Computing Threats Loom, Microsoft Updates Its Core Crypto Library
Recommendation on a Coordinated Implementation Roadmap for the transition to Post-Quantum Cryptography | Shaping Europe’s digital future
Quantum Fourier Transform (QFT) of a Single Qubit is Hadamard Transform
Below is the definition of QFT as illustrated in the YouTube lecture by Abraham Asfaw.
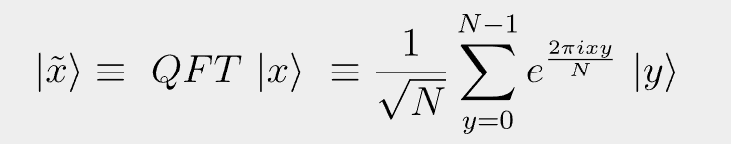
The LaTex code for the equation is as follows and also available here.
Latex
| \tilde{x} \rangle \equiv ~ QFT ~ |x \rangle ~ \equiv \frac{1}{\sqrt{N}}\sum_{y=0}^{N-1}{e^{\frac{2\pi ix y}{N}}} ~| y \rangleFor the one qubit case, N = 21 = 2: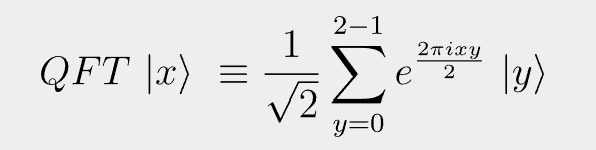
Latex
| \tilde{x} \rangle \equiv ~ QFT ~ |x \rangle ~ \equiv \frac{1}{\sqrt{}N}\sum_{y=0}^{N-1}{e^{\frac{2\pi ix y}{N}}} ~| y \rangle
Latex
\frac{1}{\sqrt{2}}\sum_{y=0}^{1}{e^{\pi ix y}} ~| y \rangle = \frac{1}{\sqrt{2}}[~e^{i \pi x 0}~ | 0 \rangle ~ + ~ e^{i \pi x 1}~| 1 \rangle] = \frac{1}{\sqrt{2}}[~|0\rangle ~+~e^{i \pi x}~|1 \rangle~]Latex
QFT~| 0 \rangle = \frac{1}{\sqrt{2}}[~|0\rangle ~+~e^{i \pi 0}~|1 \rangle~] = \frac{1}{\sqrt{2}}[~| 0 \rangle + |1 \rangle~] = |+\rangleLatex
QFT~| 1 \rangle = \frac{1}{\sqrt{2}}[~|0\rangle ~+~e^{i \pi 1}~|1 \rangle~] = \frac{1}{\sqrt{2}}[~| 0 \rangle - |1 \rangle~] = |-\rangleHence the QFT of a single qubit is essentially the Hadamard transform.
Quantum computers’ ‘ChatGPT moment’ is coming | Views | HSBC Holdings plc
South China Morning Post: Beijing urges breakthroughs in chips and quantum computing to command future
South China Morning Post: US users rush in as China opens top quantum computer to the world: state media
If you are interested in exploring Origin Wukong, you can sign up for an account at the following link:
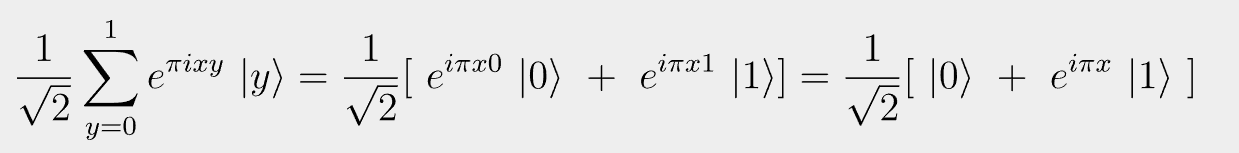
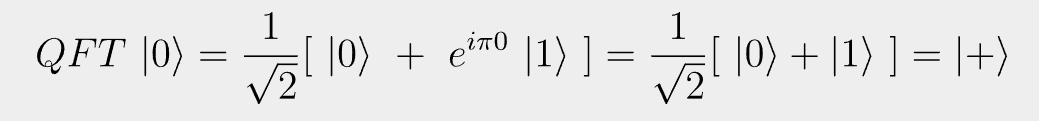
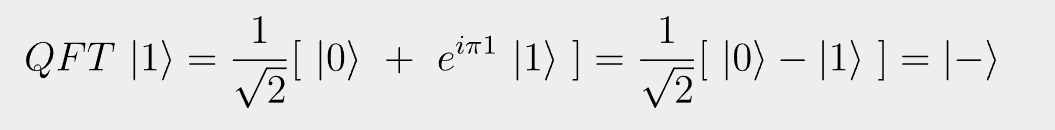
You must be logged in to post a comment.